Estimation of axial length in clinical practice
Professor Philip Morgan outlines how ocular axial length can be estimated in practice from conventional optometric measures.
A curious observation of the practice of optometry (literally ‘eye measurement’) is that assessing size of the eye does not generally feature as part of a routine eye examination. Whilst we easily recognise that +1.50DS describes a low hyperope and -9.50DS a high myope,in general, we have less understanding if an eye with axial length 28mm is small, average or large.
However, over the past few years there has been a growing realisation that excessive ocular size is associated with a range of pathological conditions (including increased levels of retinopathy,1 retinal detachment,2 glaucoma3 and cataract4) and interest in axial length as a relevant measure has been piqued not just because of the increase in myopia across the world in general5 and in East Asia in particular6–9 but also because of the growing availability of management options such as soft dual-focus contact lenses,10,11 orthokeratology lenses12–15 and pharmaceutical options.16
Of course, there is an inherent relationship between refractive error and axial length but it seems the latter is the key determinant for predicting visual impairment, according to a study of over 9,000 eyes conducted in the Netherlands.17 Specifically, in this work, the authors reported that for people 75 years and older, the risk of visual impairment was 3.8% for those with eyes of axial length 24 - 26mm compared with 91% in eyes over 30mm in length. (Figure 1.) These data show the importance of axial length as a clinical measure and reinforce the need for it to become more firmly entrenched in the optometric lexicon.
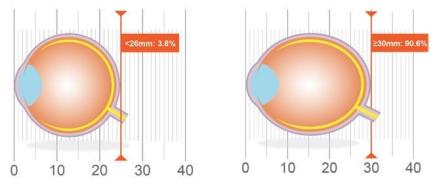
Figure 1. Association of axial length with risk of uncorrectable visual impairment (adapted from Tideman17)
Over the past 20 years, sophisticated axial length instrumentation such as the IOLMaster series (Zeiss), the Lenstar (Haag-Streit) and the Aladdin (Topcon) have become available.18 These devices are typically used to determine intraocular lens power for patients presenting for cataract surgery but have also been adopted in myopia control clinical studies.10–14,16 However, their cost of £20,000 to £40,000 may minimise uptake by clinicians with an early interest in myopia and its management. Anecdotal reports suggest that there could be fewer than 20 modern generation biometers in optometric practices across the United Kingdom.
Given the increasing need for axial length measurement and the significant cost of measurement hardware, it seemed logical to explore the potential for estimating this important metric from other, standard measures with obvious candidates being refractive error and corneal curvature - values which can be readily captured at any eye examination.
The first step in this process was to identify a dataset which provided axial length, refractive error and corneal curvature so that the relationship between the three could be explored. To do this, data from a recently published study on the MiSight® 1 day lens10 (a novel dual focus lens designed for myopia management) were employed. This study examined the progress of 144 subjects, aged 8-12 years at commencement, over three years. Topography and axial length measures were evaluated annually with an IOL Master (Zeiss) and cycloplegic and non-cycloplegic refractive errors were determined with a WR-5100K or WAM-5500 autorefractor device (Grand Seiko Co).
The best fit relationship for axial length was

where A is axial length in millimetres, k is mean anterior corneal radius of curvature and S is the best spherical refractive error at the corneal plane.19
The relationship here was found to be highly correlated with r2 = 0.83 but a more important consideration is the 95% limits of agreement which predict the confidence a user can place in the derived value for axial length. These were determined to be ±0.73mm or ±3.0% of an average axial length measurement. This suggests, therefore, that 95% of values derived from the formula will be within about three-quarters of a millimetre of the ‘true’ axial length (as measured by an interferometric biometer). Similar findings were found when the non-cycloplegic findings were examined. Importantly, these limits of agreement were much lower (better) than when refractive error only was used to estimate axial length (±1.26mm) indicating that adding corneal curvature measures into the formula provides for a much improved prediction.
To test this formula on a different dataset - using a different group of subjects and protocol - information from the Northern Ireland Childhood Errors of Refraction (NICER) study of Saunders and colleagues 1920–22 were used. Here, data for 1,046 subjects were analysed. Using the same formula, the 95% limits of agreement were about the same as for the MiSight® 1 day lens study at -0.73 to +0.99mm (an average of ± 3.7%).
Overall, then, this simple formula provides a reasonable estimate of absolute axial length of the eye. With the extreme range of axial lengths in adult humans ranging from 15 to 38mm (and with the mean ± two standard deviations of 21 to 26mm)17, estimating axial length to 0.73mm is good, akin to estimating someone’s height to within an inch or two. It is sufficiently good, for example, to place a patient into one of the risk categories described by Tideman et al. of: less than 24mm, 24-26mm, 26-28mm, 28-30mm and greater than 30mm17 and the formula appears to be somewhat robust to data presented from different sources.
A working example here is two patients each with a spectacle prescription of -3.50DS at a back vertex distance of 12mm. Evaluation of their superficial refractive error might categorise them at medium level of myopia-related risk of visual impairment. However, if one patient has steep corneas (7.3mm) then their estimated axial length is 23.9mm putting them in the lowest risk group of Tideman et al.17 If the other has flat corneas (8.3mm), then they move two ‘risk groups’ higher with an estimated axial length of 26.2mm. Clearly, relying on refractive error alone does not provide the full picture, especially in the cases of very steep or very flat corneas.
However, the calculation is not sufficiently sensitive to track changes in axial length over time or to carefully monitor the impact of different myopia treatment modalities. The confidence limits of about 0.73mm is at the upper end of what might be expected for the change in a child’s axial length over three years.10 This means that the predictions from the formula are too ‘noisy’ for detailed tracking of changes over time; again, a system to estimate a human height to within an inch or two is unlikely to be very helpful when monitoring a child’s growth between, say, the ages of 10 and 12 years . In contrast, commercial biometers have 95% confidence limits of around ±0.06mm or ~0.25% or better.23,24
In summary, understanding axial length is an increasingly important part of optometric practice especially with management options becoming approved by regulators and available in the UK market. The formula developed in this initiative provides extra clinical information for optometrists and opticians in the community considering myopia management, and can assist in clinical decision making. It can also provide a greater understanding of the importance of axial length as a relevant contemporary optometric measure and can serve as a useful discussion point for patients and their parents - and give an indication around the urgency of any myopia management strategy. However, practitioners wishing to to closely track axial length over time should consider using a commercial biometer.
Acknowledgement
This work was supported by CooperVision, Inc.
References






